The brief is as followed. To calculate a complex surface, it is possible to use the Monte-Carlo approximation to have a number close to reality. First we will check whether it’s true or not by comparing our values with the real one. And then we will use Galapagos to seek for the best result.
What is Monte-Carlo.
Monte Carlo methods, also known as Monte Carlo experiments, are a category of computational algorithm that relies on repeated random sampling to produce numerical results. The underlying idea is to use randomness to solve problems that are, in theory, deterministic. They are frequently used in physical and mathematical problems and are especially useful when other approaches are difficult or impossible to use. Monte Carlo methods are commonly used to solve three types of problems: optimization, numerical integration, and generating draws from a probability distribution.
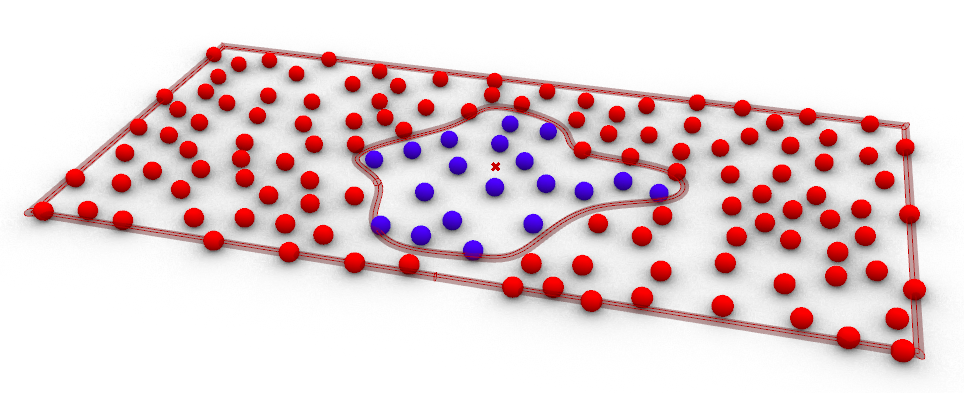
We will here use this method to evaluate the surface of a complex shape. The idea is to throw balls and count how many are inside the complex shape how many are outside. The proportion of inside/outside would be the same as the proportion complex’s surface area, reference surface area.
Let’s do it in Grasshopper.
Preparing the shapes.
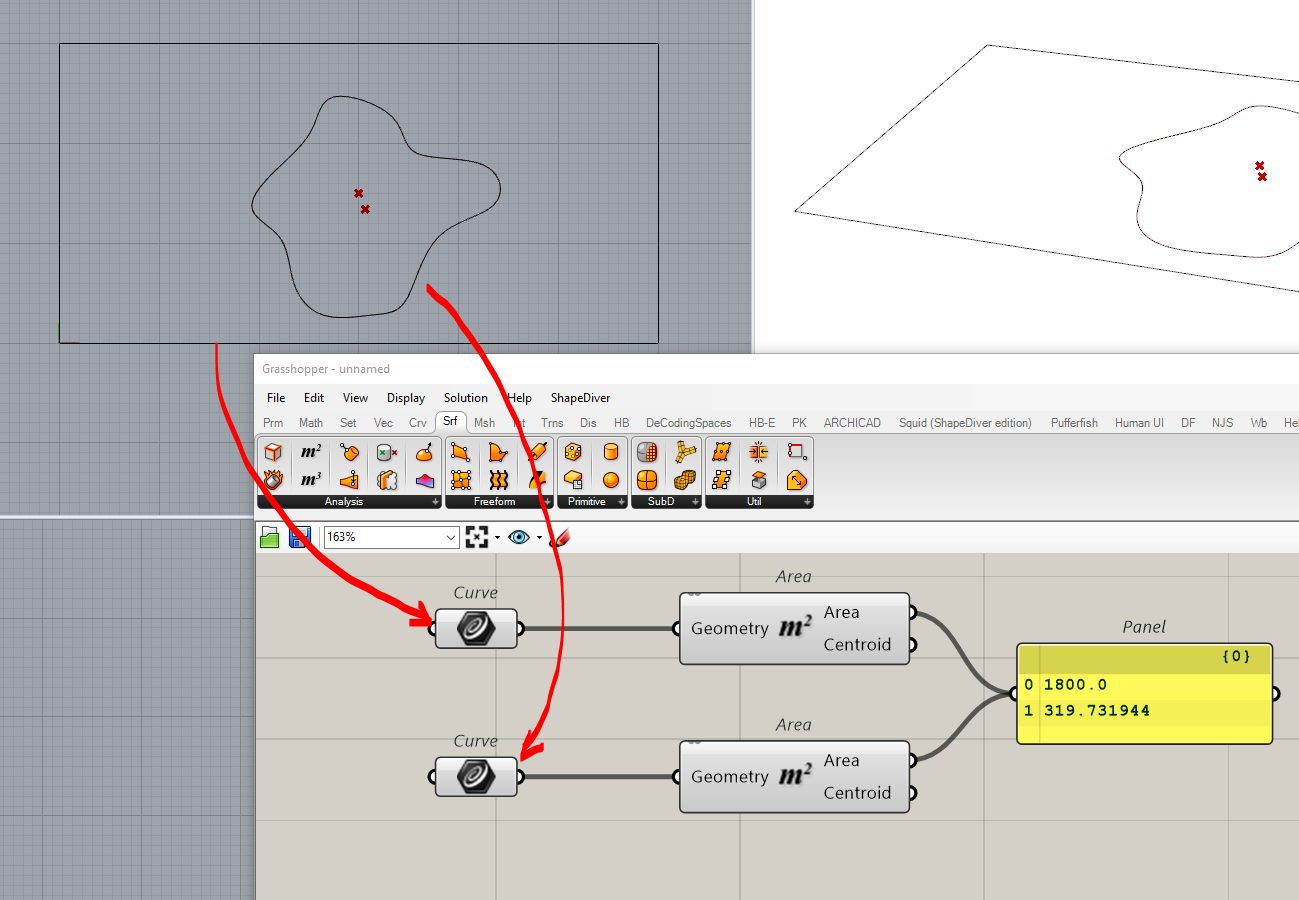
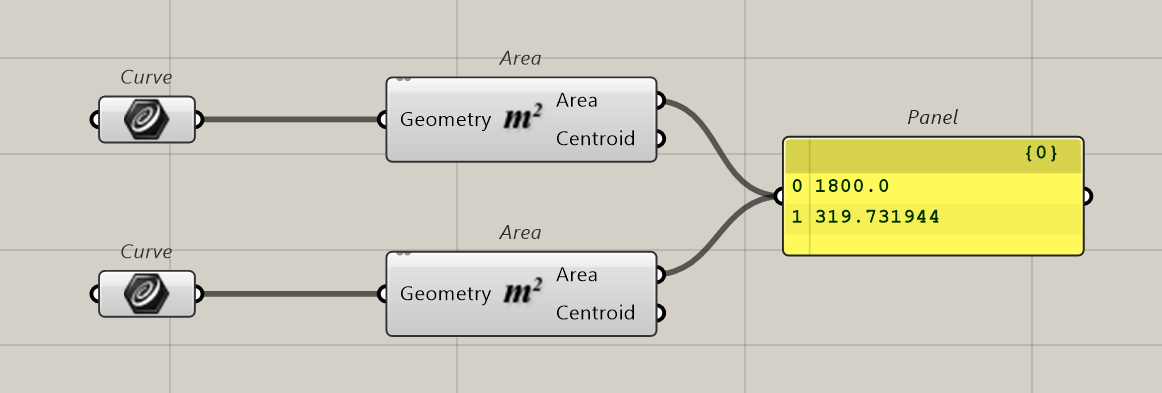
First we create the reference shape and the complex one in Rhino.
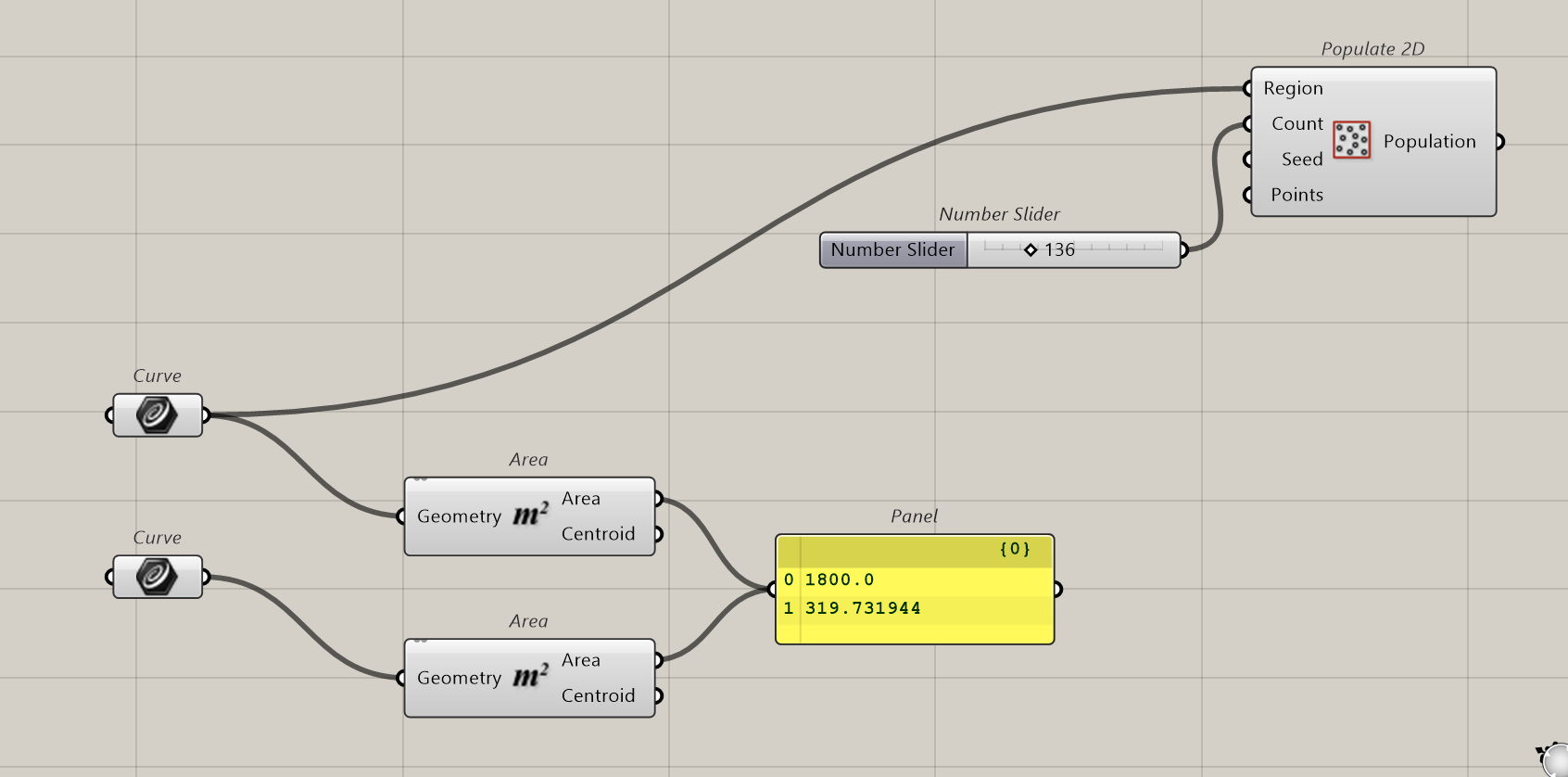
We then import the 2 shapes in Grasshopper and we check the two areas…
Throwing balls
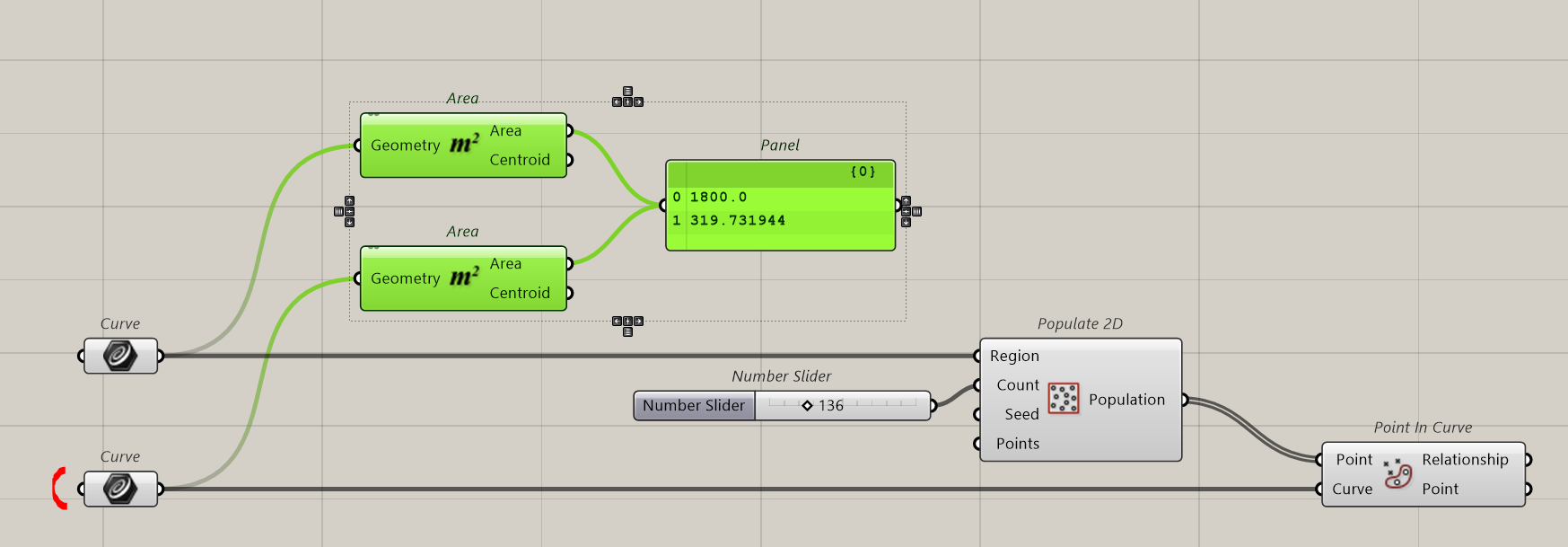
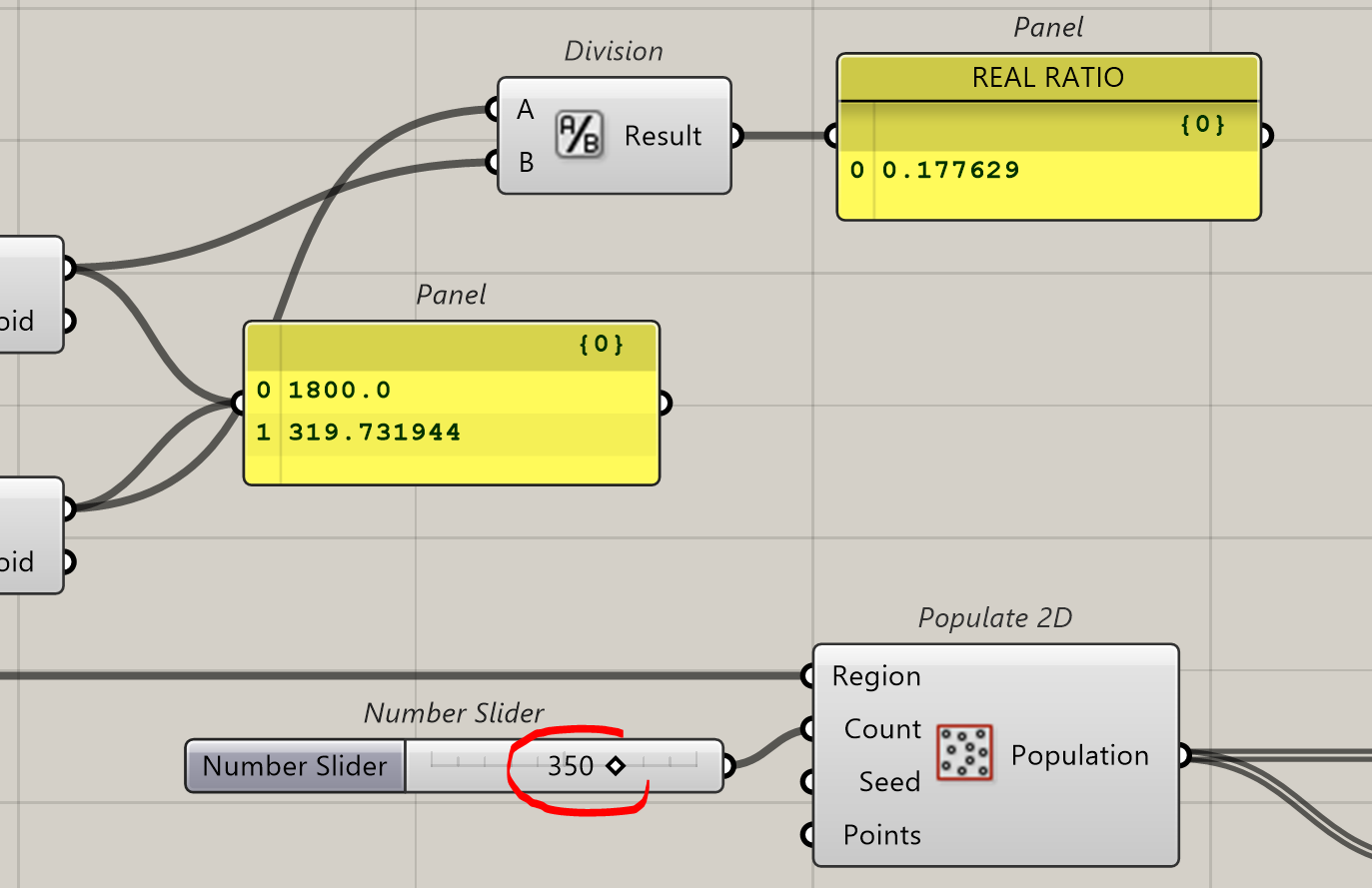
We will populate the big rectangle with points. The count will be set with a slider ranging from 50 to 500, the Region is the rectangle.
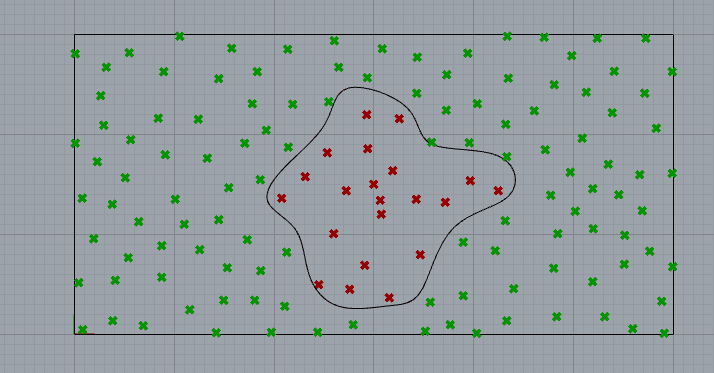
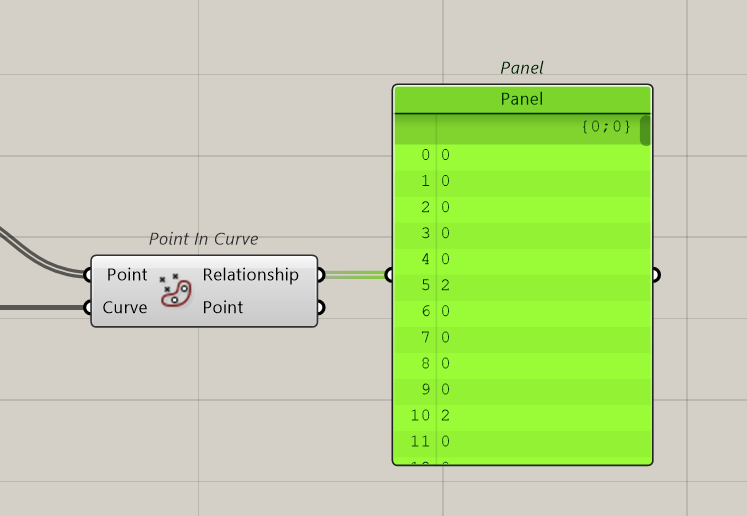
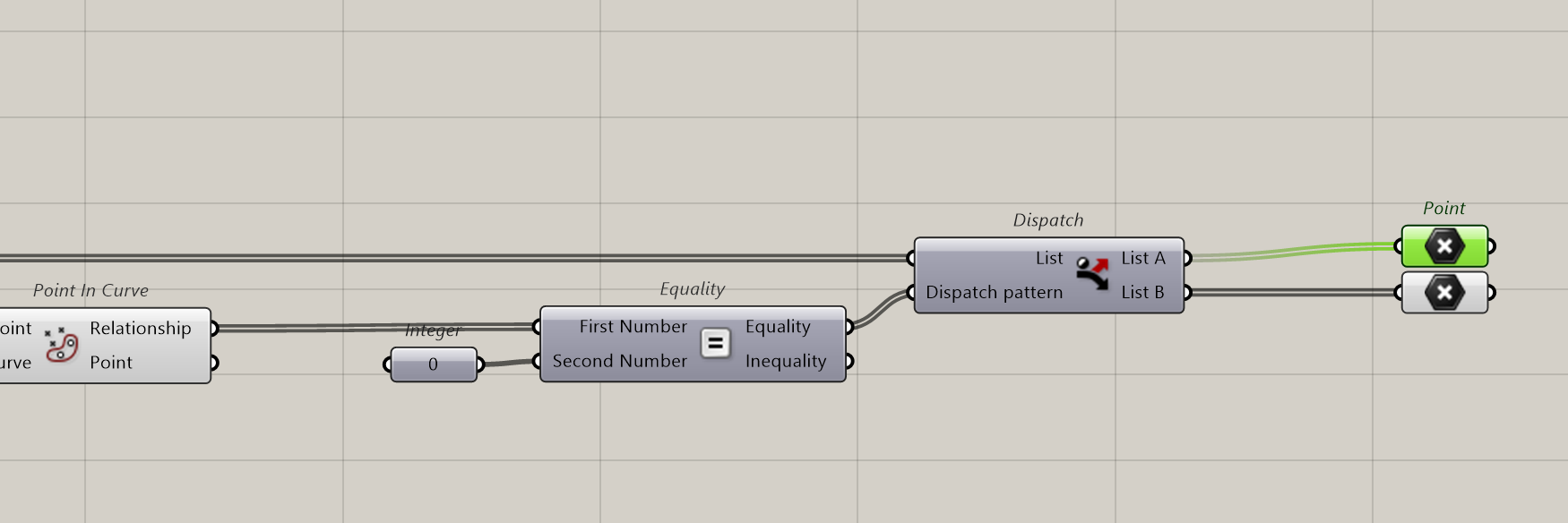
We now check which points are inside the complex shape and which are outside. For that we use the Point In Curve component
Relationship gives us 3 possibilities: 0 = Outside, 1 = Coincident, 2 = Inside.
We need to filter the list of points with this three possibilities.
We could also filter the points that are coincident. Let’s try mixing coincident with inside. This way we have only two lists.
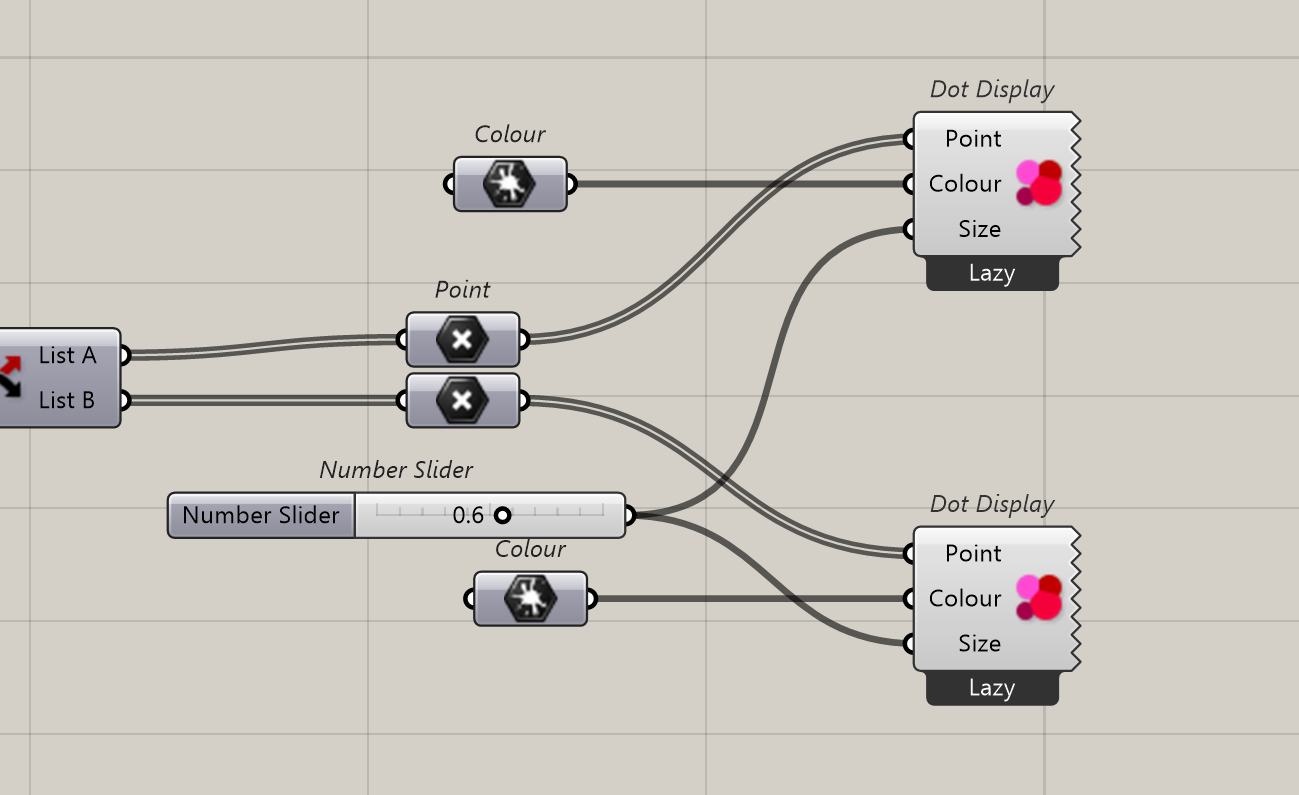
Ok, let’s count our points and verify the theory. But before that we can pimp a little our points.
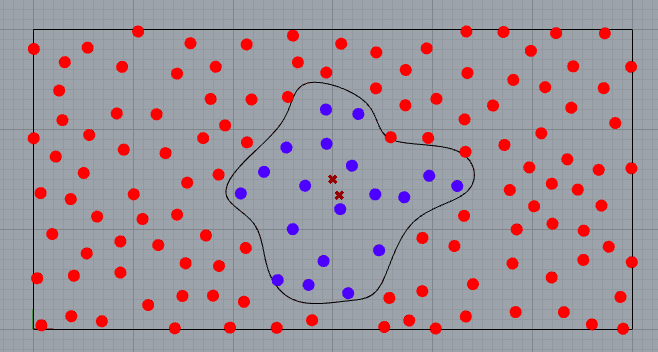
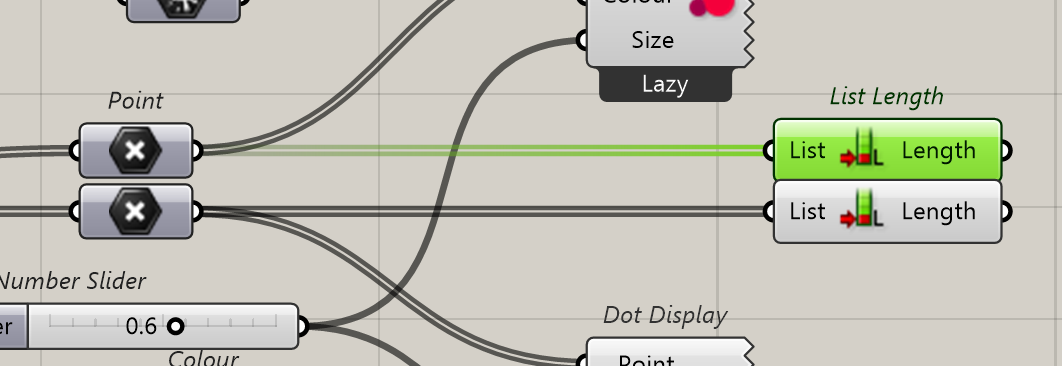
We count
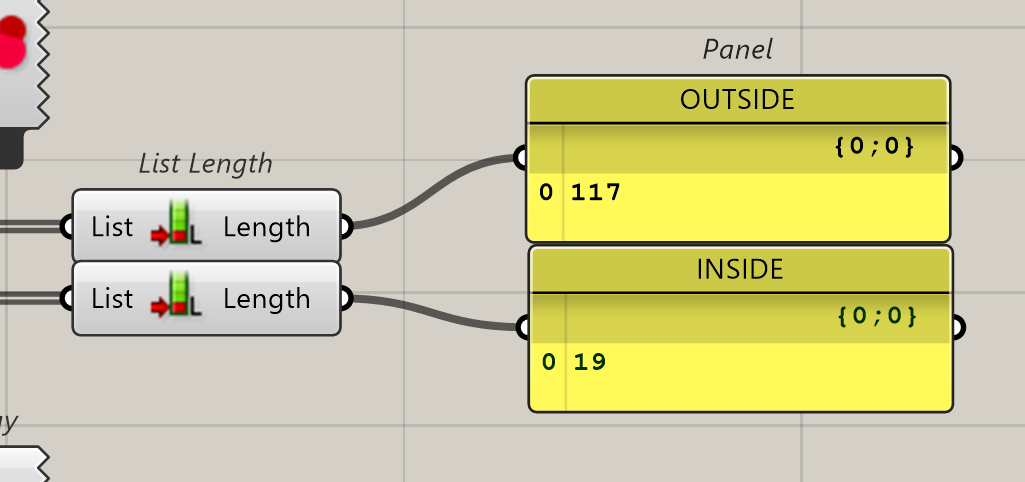
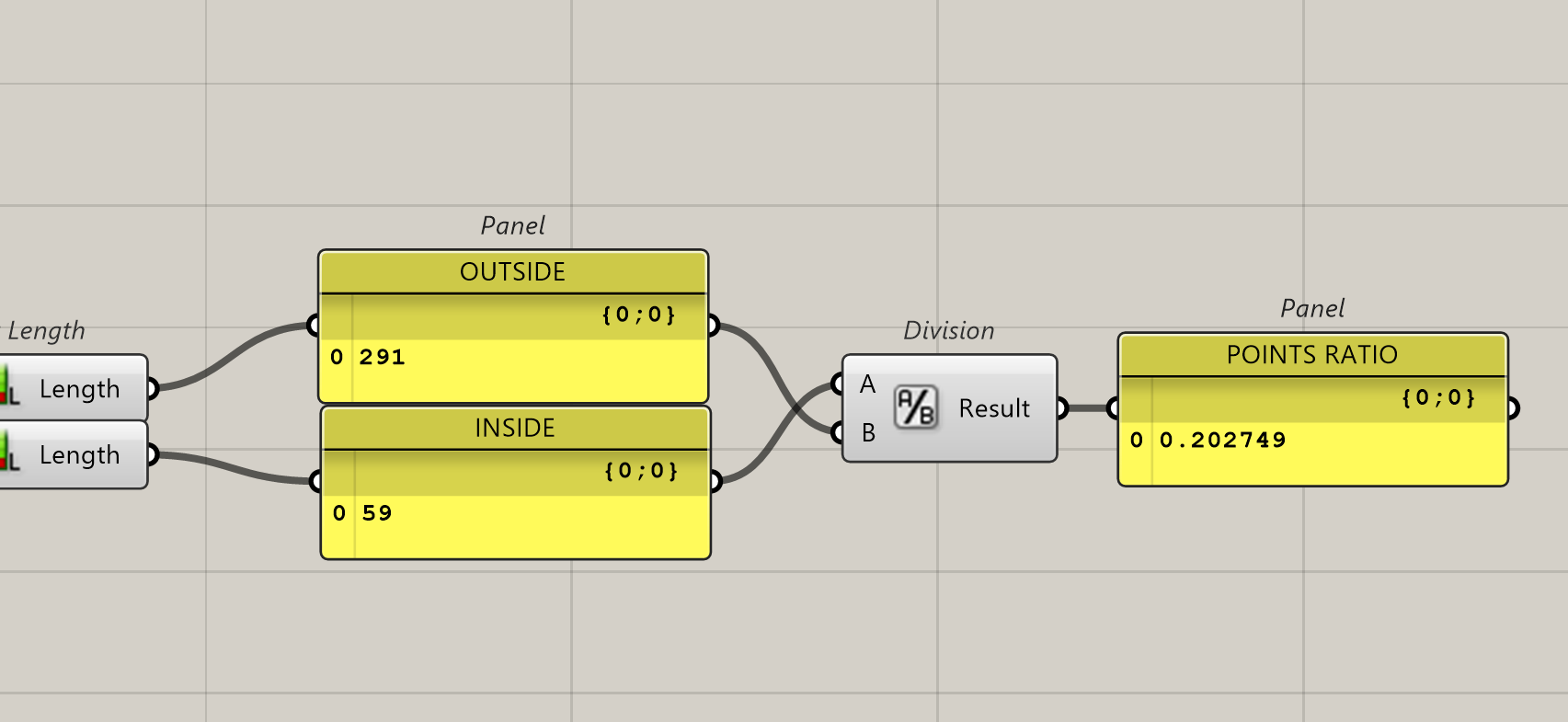
So, if we summarise, we have 19 points inside and 117 outside, this is a ratio of 19/117 = 0.1624. If we compare with the real surfaces we will have 319.73/1800= 0.1776. Close…not quite accurate but close. Monte-Carlo will give us a surface of 1800*0.1624= 292,32 instead of 319.
Is it a matter of number of points. We increase the number of points. Go for 350.
More is not better
Using Galapagos
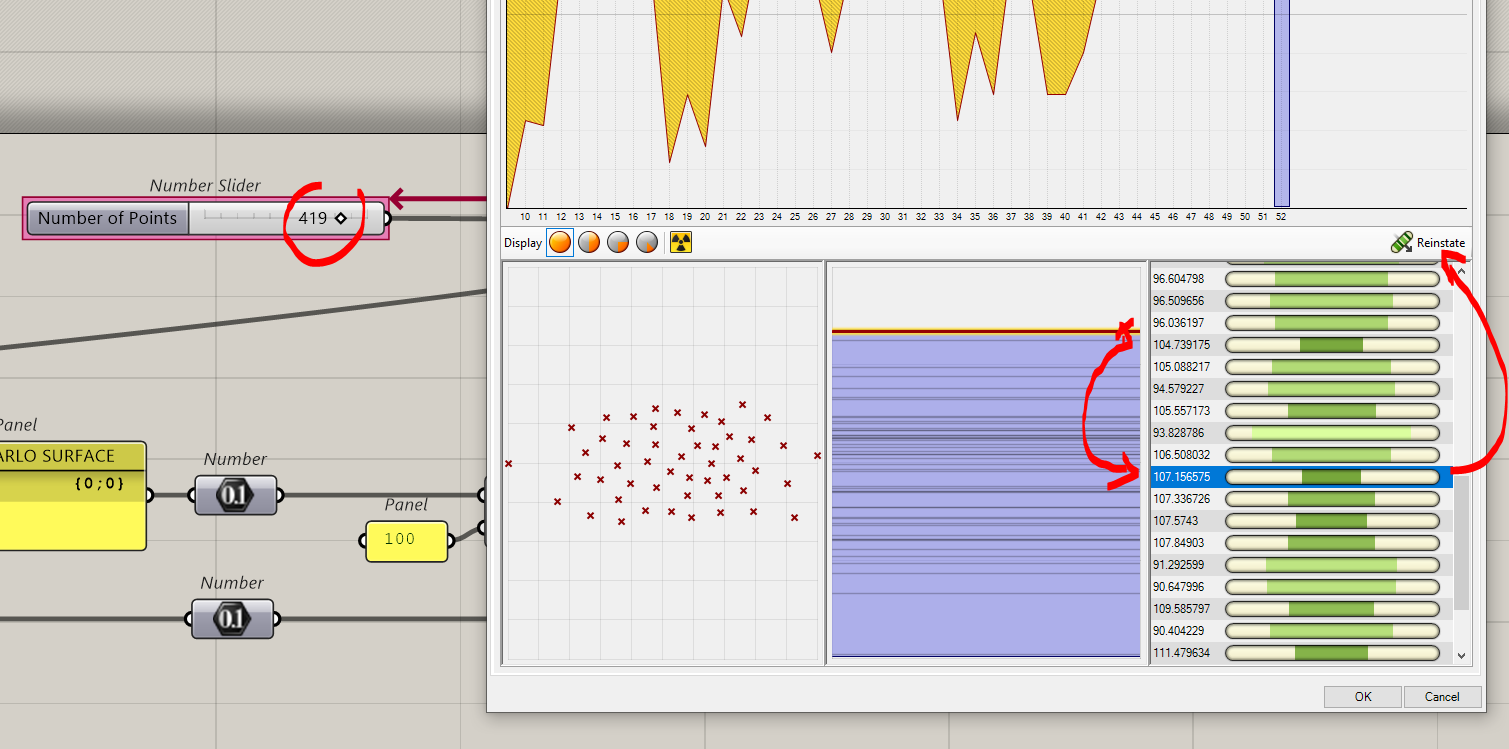
Using Galapagos, we will determine which random number produces the best results, which is somewhat contradictory. Anyway.
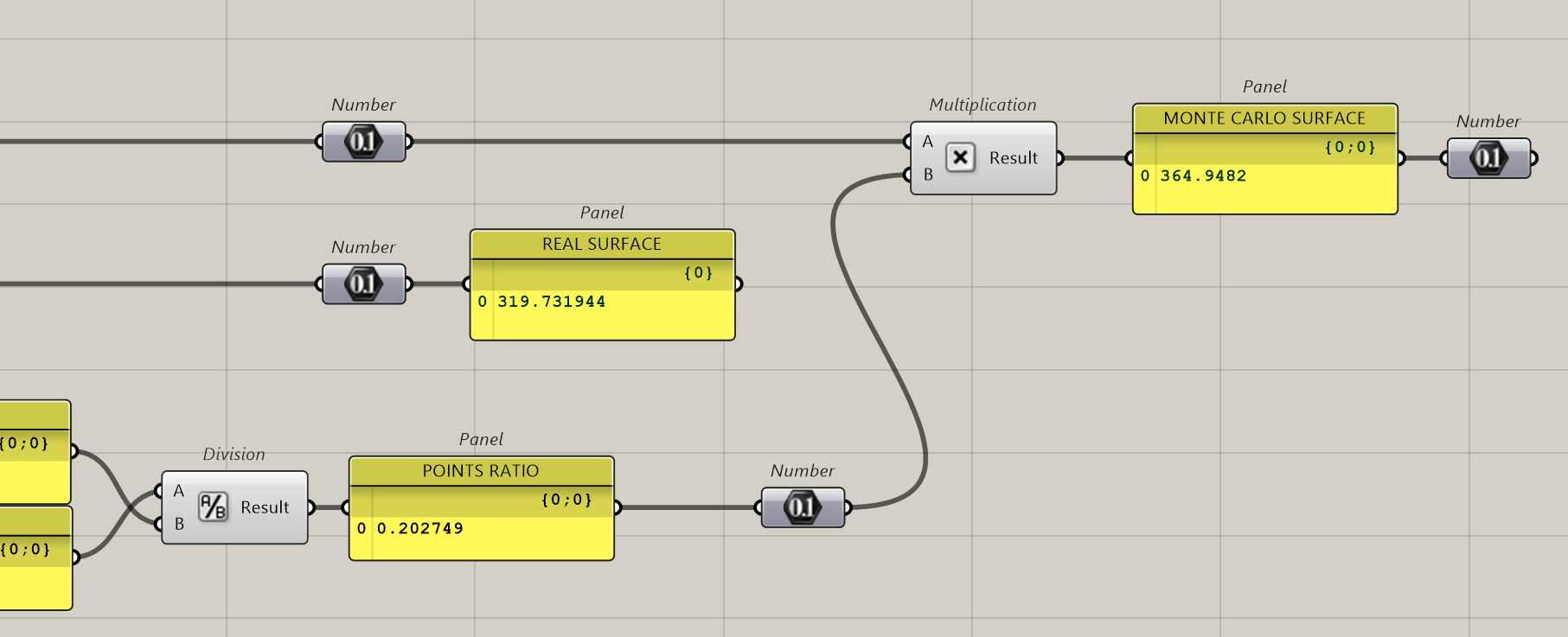
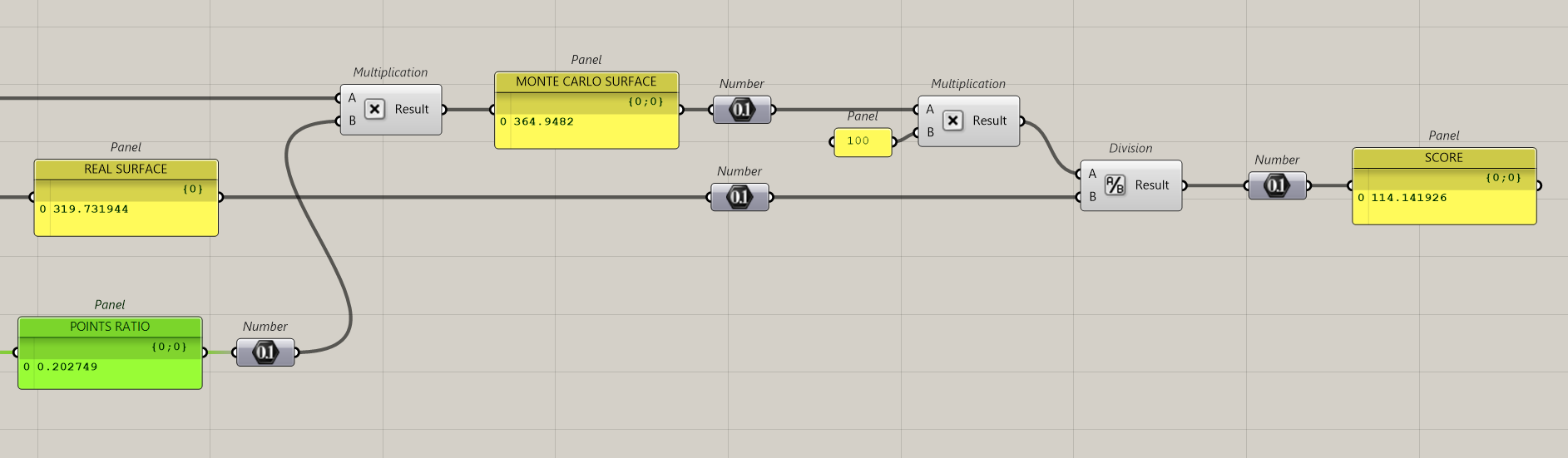
We compare now the real surface with the Monte Carlo one. If it fits, it has a score of 100%. So we need to define which number of points reaches or approaches the score of 100%.
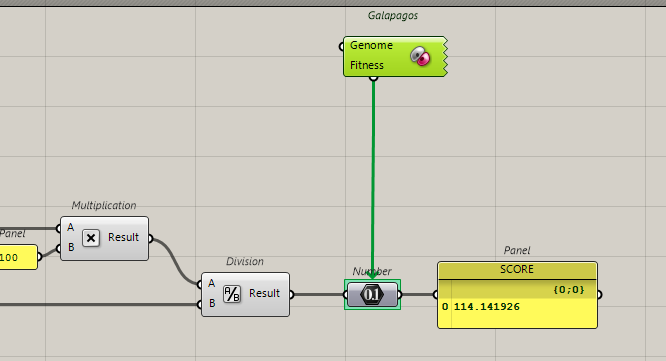
OK, we grab the real surface, we calculate the Monte-Carlo surface and we calculate the score.
A simple % setting
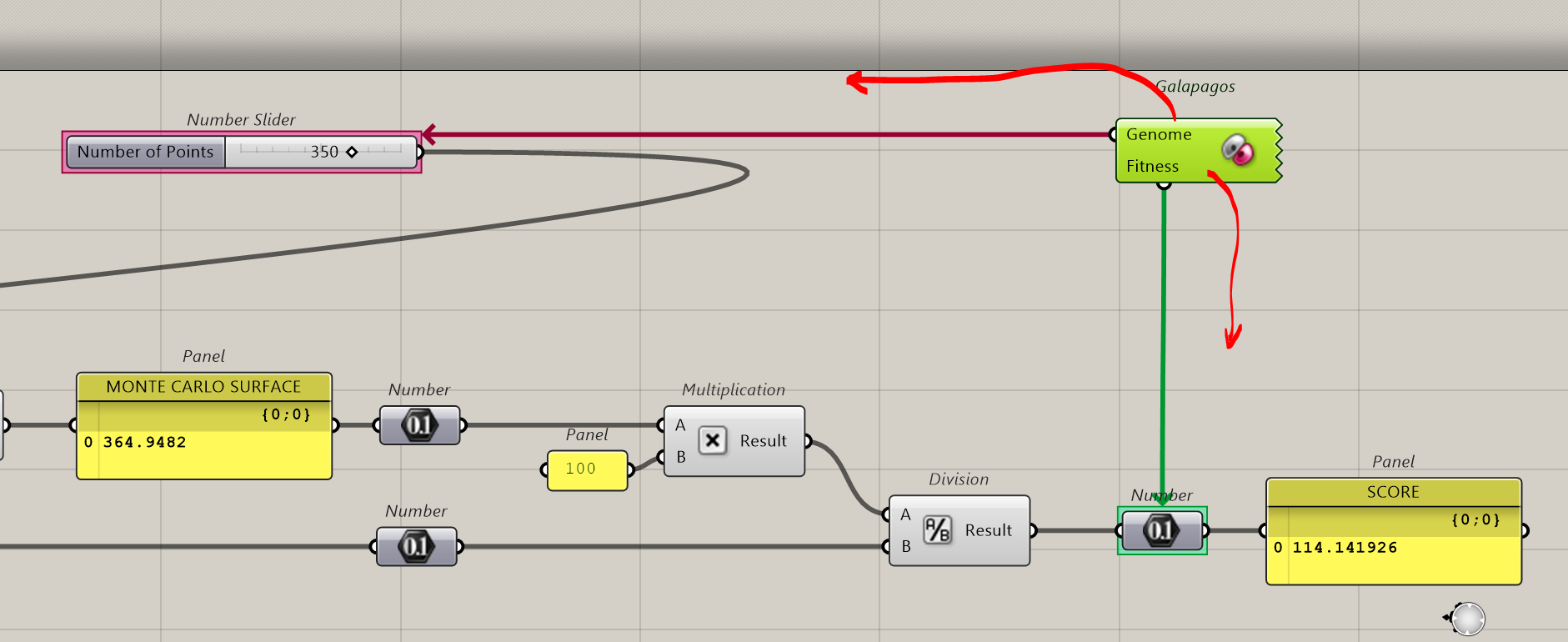
Now we have to connect Galapagos to the slider that creates the points and to the score we have.
And to the Slider (it has been moved closer to Galapagos to better see the connections)
Remember to connect Galapagos, it’s from Galapagos to the desired component
Double click on Galapagos
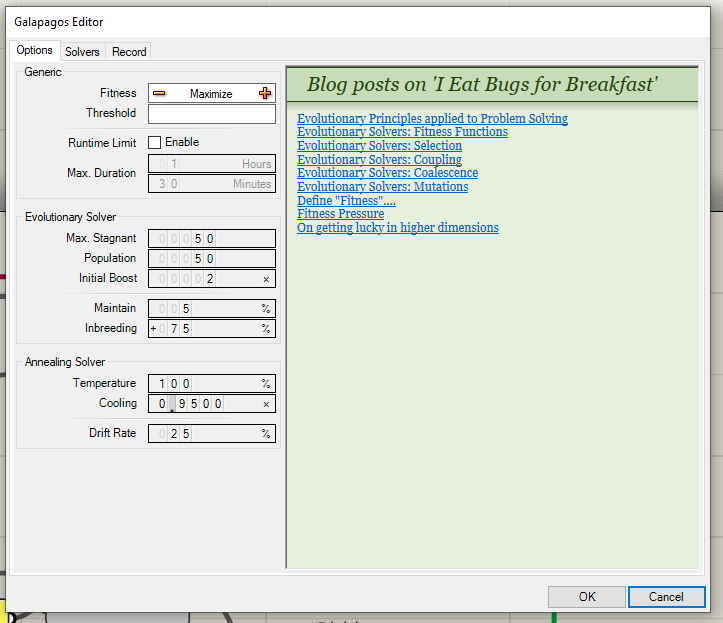
Instead of Maximize, we set to 100. This is the score we’re looking for.
Solver Start Solver

Solutions are tested
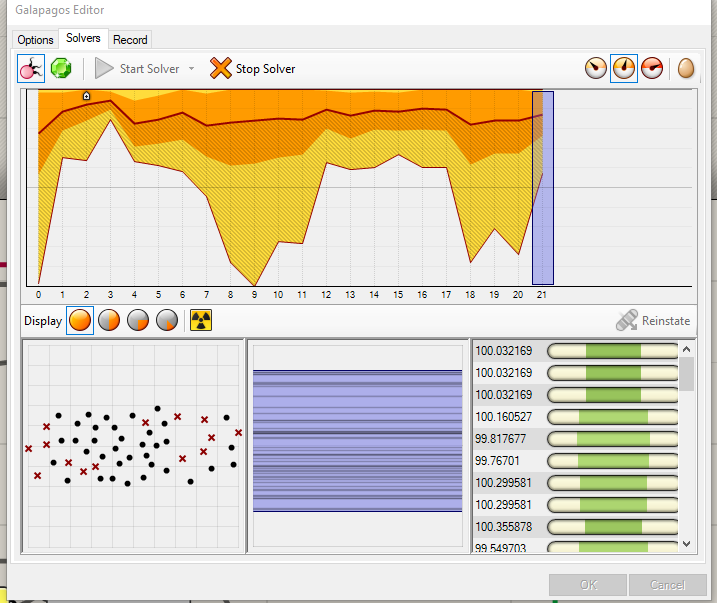
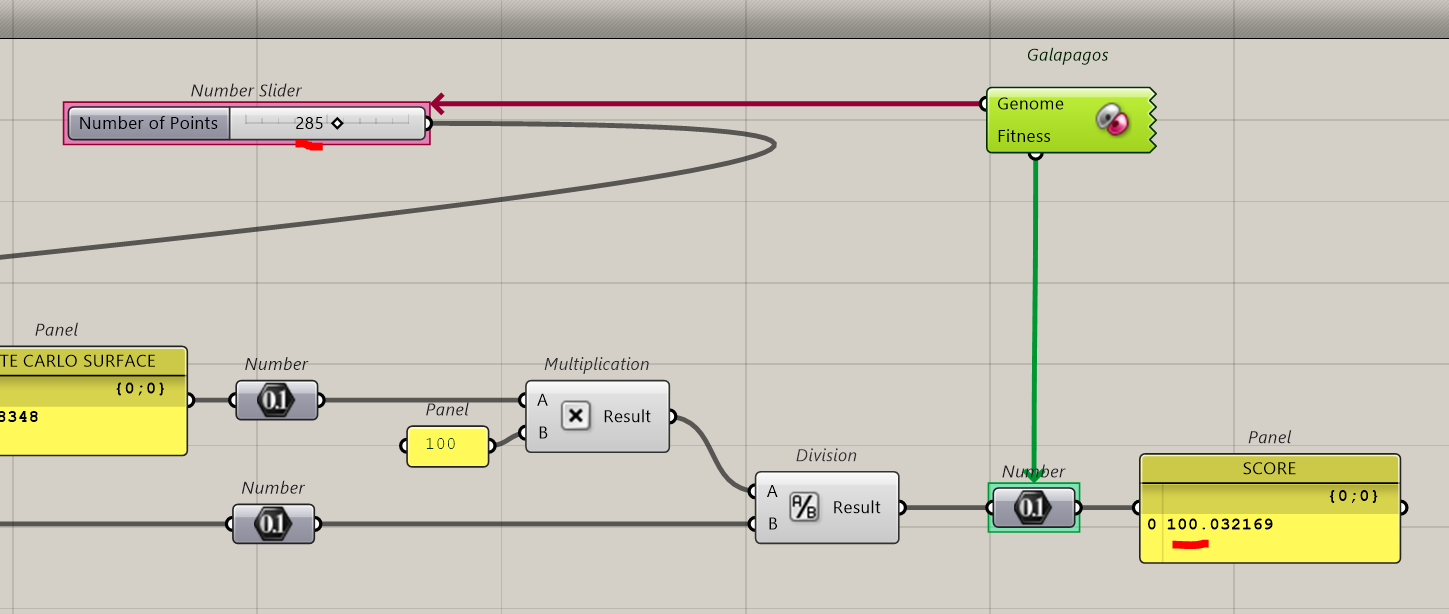
The best score is 100.032 very close to the real result.
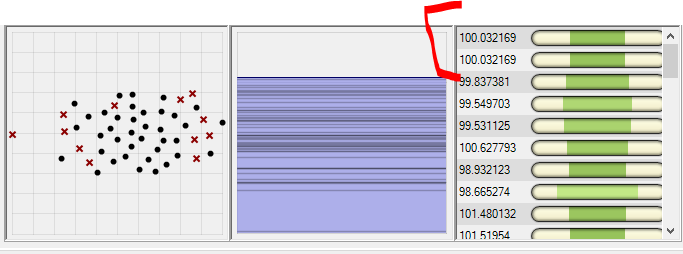
It has been obtained with 285 points

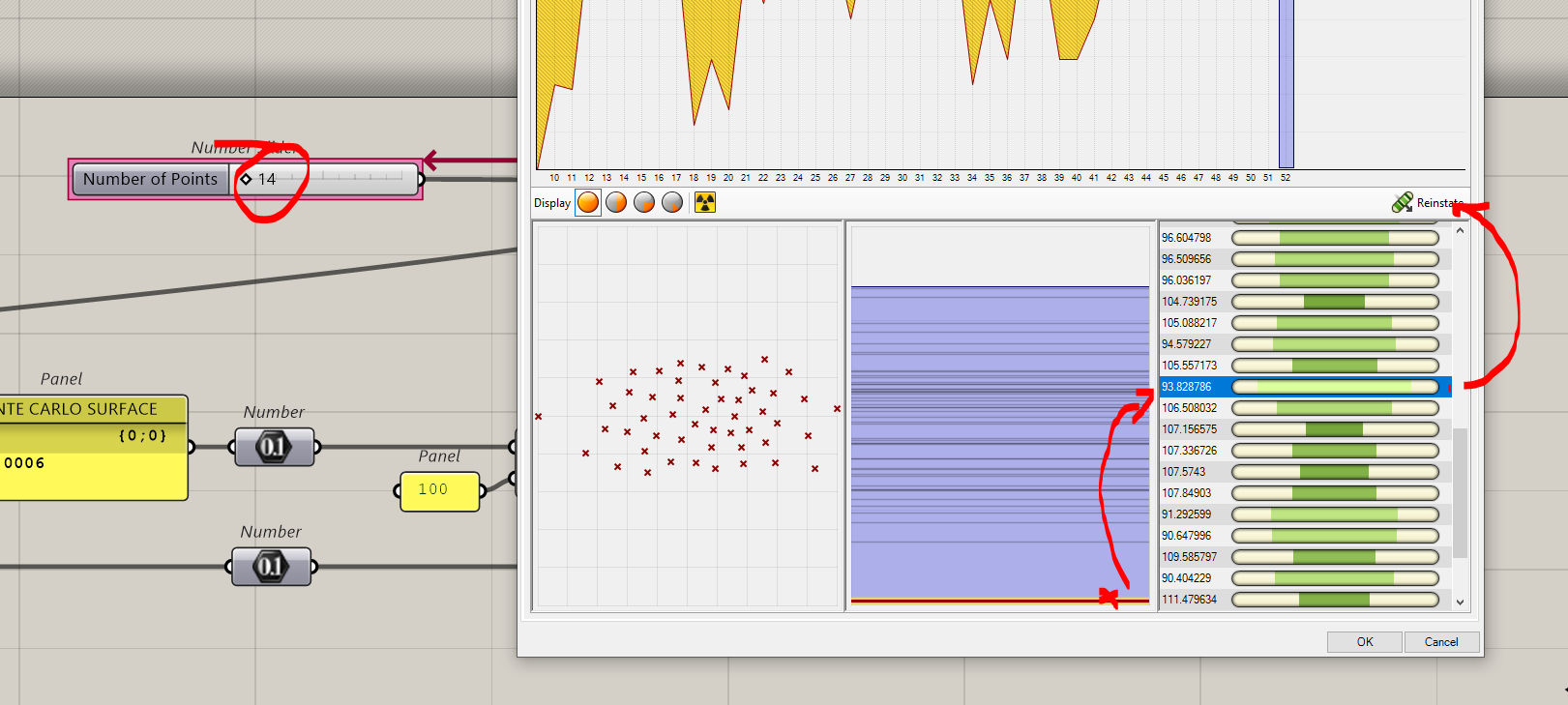
Let’s check the worse results
And
That’s all for that.




Exercise tres pertinant.